Regularization

안녕하세요? 이번 시간에는 Regularization에 대해서 알아 보도록 하겠습니다.

우리가 모델을 만들 때, 많은 분들이 Overfitting을 경험 해 보셨을 것 입니다. 여러분들은 Overfitting을 경험할 때, 다음과 같은 것들을 시도 해 볼 것입니다.

• 모델의 크기를 줄인다. (네트워크의 깊이, 노드 갯수 등등)
• 데이터의 크기를 늘린다.

하지만, 이 외에도 다른 방법들이 있습니다. DropOut과, Regularization이 있는데요. 이는 모델의 크기의 조정 없이, 데이터의 크기를 늘릴 필요 없이 사용 가능한 방법 입니다.

오늘은 학습 모델의 파라미터 크기를 규제 함으로써 작동하는 Regularization에 대해서 알아 볼 예정입니다. 한국말로 번역하면 정규화라고 합니다.

그럼 Normalization은요?

논문을 보다 보면, Normalization과 Regularization에 대해서 이야기를 하는 경우가 많은데, Normalization도 한국말로 번역하면 정규화입니다. 하지만, 여기서 이야기 하는 의미는 다릅니다.

Normalization은 Dataset에 적용하는 것입니다. 데이터의 한쪽 Feature가 너무 커버리면 데이터의 수렴이 잘 이루어 지지 않습니다. 똑같은 학습률을 가지고, 한 쪽 Feature은 크게, 다른쪽 Feature를 적게 학습 되는 경우가 발생 하기 때문이죠. 그렇기 때문에 데이터를 Normalization 하여, 각 Feature가 중구난방으로 학습 되는 것을 방지 합니다. 자세한 내용은 해당 포스트를 참고해 주세요!

Overfitting

우리는 Overfitting에 대해서 다음과 같이, 모델의 용량이 데이터 셋에 비해 너무 크기 때문에 발생하는 일이라고 생각 합니다.

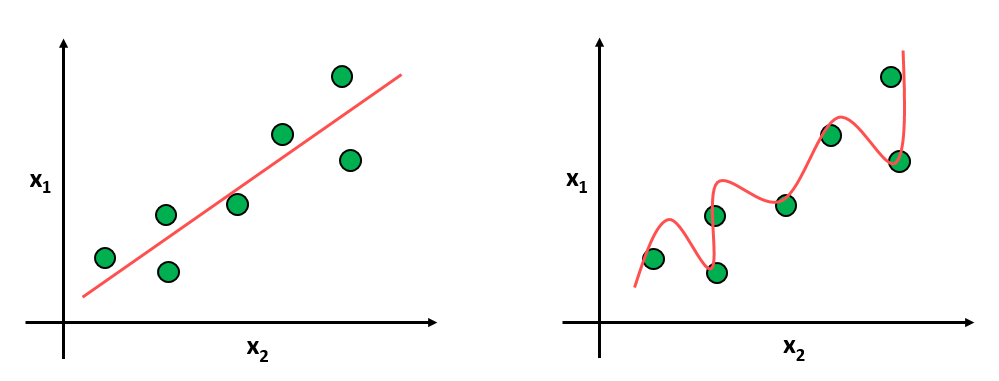
그런데 1차원 적으로 해석해보면, Overfitting은 특정 파라미터가 유난히 큰 값을 가질 때 발생합니다. 위에 그림에서 볼 수 있듯이 만약 한 쪽 파라미터가 데이터 셋에 모델을 맞추기 위해 유난히 큰 값을 가지게 되면 Overfitting이 발생 합니다.

그러면 우리는 어떻게 하면 될까요? 특정 파라미터가 큰 값을 가지지 않도록 규제를 해주면 됩니다.

L1 Regularization

L1 Regularization은 일반 Cost Function식에 가중치 $w$에 대한 L1 Norm 규제 항을 적용 합니다. 규제항을 미분 하게 되면, $w$의 부호 벡터 ($sign(w)$)가 빠져 나오게 됩니다. 이를 학습에 적용하면, ($sign(w)$)는 -1, 1 밖에 존재 하지 않으므로, 학습에 큰 관여를 하지 않는 항이 0이 되어, 특징 선택 의 효과가 있습니다.

여기서 $L(y, \hat{y})$는 기존 Cost Function을 의미 합니다.

L2 Regularization

L2 Regularization 일반 Cost Function식에 가중치 $w$에 대한 L2 Norm 규제 항을 적용 합니다. 규제항을 미분 하게 되면, $2w$가 나오게 됩니다. 이를 학습에 적용하면, 학습률 $\lambda$에 $2w$를 곱한 만큼 값이 줄어들게 되는 효과를 가져, Feature를 원점으로 모아주는 역할을 합니다.

우리는 학습 과정에서 Test Error가 최소가 되는 값을 하이퍼파라미터로 지정하여, 학습의 능률을 높이는 것이 중요 합니다.