수식과 코드로 알아보는 로지스틱 회귀

저번 시간에는 선형 회귀에 대해서 배워 보았습니다. 선형 회귀는 $D$ 차원의 벡터 독립 변수 $X$ 가 존재한다고 가정 하면, 그에 따른 종속 변수 $y$ 가 있다고 가정하여, 선형 상관 관계를 모델링 하는 것이라고 배웠습니다. 예시 코드를 보겠습니다.

from random import random
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
import matplotlib.pyplot as plt

X = np.random.random((20, 1)) * 20
Y = X * 2 + 1 + np.random.random((20, 1)) * 10

lin = LinearRegression()
lin.fit(X, Y)

plt.title("Linear Regression")
plt.scatter(list(map(lambda x: x[0], X)), list(map(lambda y: y[0], Y)), c="#000000")
x1, y1 = [0, 20], [lin.coef_[0] * 0 + lin.intercept_, lin.coef_[0] * 20 + lin.intercept_]
plt.plot(x1, y1, color='blue')
plt.show()

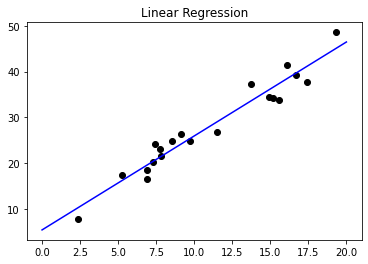
랜덤한 데이터에 대한 선형 회귀

하지만, 범주형 변수에 대해서 생각을 해 보겠습니다. 예를 들어, 50점 이상이면 합격, 이하면 불합격이고, 이를 합격일 시 1로, 불합격일 시 0으로 나타 내 보겠습니다. 이러한 데이터에 선형 회귀를 적용 하게 된다면, 어떻게 될까요?

X = [[49], [60], [12], [43], [97], [40], [65], [10]]
Y = list(map(lambda x: [x[0] // 50], X))

lin = LinearRegression()
lin.fit(X, Y)

plt.title("Linear Regression")
plt.scatter(list(map(lambda x: x[0], X)), list(map(lambda y: y[0], Y)), c="#000000")
x1, y1 = [0, 100], [lin.coef_[0] * 0 + lin.intercept_, lin.coef_[0] * 100 + lin.intercept_]
plt.plot(x1, y1, color='blue')
plt.show()

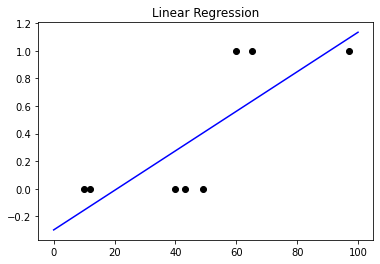
어? 심상치 않은데?

대충, 뭔가 잘못되었다는 느낌은 듭니다. 그렇습니다. 범주형 변수는 선형 회귀를 통해 학습 하기 힘든 변수라는 것입니다. 그렇다면 범주형 변수는 우리가 어떻게 처리 하여야 할까요?

로지스틱 회귀

로지스틱 회귀의 아이디어는 다음과 같습니다. 일단 그 전에 시그모이드 함수에 대해 알아 보겠습니다. 시그모이드 함수는 세상의 범주형 변수가 특정 결과를 갖는 확률은 S형 곡선을 가진다는 것에서 착안 되었습니다. 또한, 이 함수는 미분이 가능하여, 경사 하강법이 시행 가능합니다. 시그모이드 함수의 식은 다음과 같습니다.

y = \frac 1 {1 + e^{-x}}

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-8, 8, 100)
sig = 1 / (1 + np.exp(-x))

plt.title("Sigmoid Function")
plt.plot(x, sig)
plt.show()

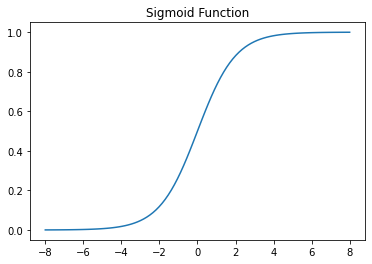
딥러닝 기초를 하신 분이라면, 구면일 것 입니다.

일단, 선형 회귀에서 한것 처럼 식을 세워 보겠습니다. 만약 0과 1중, 1일 확률을 정의해 보겠습니다. 하지만, 확률의 범위는 0~1 사이이므로, **승산(odds)**와 로그를 이용하여, 좌변의 범위가 음의 무한대부터, 양의 무한대 까지 가능하도록, 식을 다음과 같이 바꿔 써 보겠습니다.

\log{\frac {P(Y=1|X=\vec{x})} {1-P(Y=1|X=\vec{x})}} = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_px_p = \vec{\beta}^T\vec{x}

그 다음, $P(Y=1|X=\vec{x})$ 를 $p(x)$ 로, 우항을 $a$ 로 치환하면,

\frac {p(x)} {1-p(x)} = e^a

p(x) = \frac {e^a} {1+e^a} = \frac 1 {1+e^{-a}}

이를 통해 알고 있는 것은, 범주가 두 개인 분류 문제중, 특정 답이 나올 확률은 시그모이드 함수로 표현이 가능하다는 것입니다.

이항 로지스틱 회귀가 결과를 반환하는 방법

이항 로지스틱 모델에, 입력벡터 $x$ 를 넣으면 범주 1에 속할 확률을 반환해 주려면, 가장 간단하게 확률 값을 구할 수 있는 방법은 다음과 같습니다.

P(Y=1|X=\vec{x}) > P(Y=0|X=\vec{x})

좌변을 $p(x)$ 로 치환 하면 다음과 같습니다.

p(x)>1-p(x)

\frac {p(x)} {1-p(x)} > 1

\log {\frac {p(x)} {1-p(x)}} > 0

\therefore \vec {\beta}^T \vec {x} > 0

시각화 하면 다음과 같은 결과를 도출 할 수 있습니다. 위에서 시그모이드 함수를 도출 한 결과와, 이항 로지스틱 회귀의 결과 반환을 통해서 알 수 있는 결과는, $\vec {\beta}^T \vec {x}$ 은, 로지스틱모델의 결정경계라고 할 수 있다는 것입니다.

출처: ratsgo님의 블로그

이항 로지스틱 회귀 예시 코드

그럼, 한번 scikit-learn을 이용하여, 예시 코드를 한번 학습 해 볼까요?

일단 먼저 모듈을 import 해 줍니다.

from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt

그 다음, 데이터를 임의로 생성 해 보겠습니다. y는 x[0] * 2 + x[1] 가 150 이상일 경우 1을 나타냅니다.

x = []
y = []

for i in range(100):
  for j in range(100):
    x.append([i, j])

x = np.array(x)
np.random.shuffle(x)

for i in range(10000):
  if x[i, 0] * 2 + x[i, 1] > 150:
    y.append(1)
  else:
    y.append(0)

y = np.array(y)

이제, LogisticRegression() 객체를 이용하여, 데이터를 학습시킬 시간입니다. 학습을 시킨 후에, 앞에 있는 데이터 30개를 따로 추출하여, 값을 해당 모델을 이용해 예측 해 본후, 이를 시각화 해 보았습니다.

lr = LogisticRegression().fit(x, y)
test_x = x[:30]
test_y = lr.predict(test_x[:, :])

for i in range(30):
  if test_y[i] == 0:
    plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='red')
  else:
    plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='blue')

print(lr.coef_, lr.intercept_)
x1, y1 = [-lr.intercept_ / lr.coef_[0][0], (-lr.intercept_ -lr.coef_[0][1]*100) / lr.coef_[0][0]], [0, 100]
plt.plot(x1, y1, color='black')
plt.show()

학습이 잘 된 모습

이렇게, LogisticRegression 의 coef_, intercept_ 어트리뷰트를 통해 내부 가중치를 알 수 있었고, [저번 시간](https://justkode.kr/machine-learning/linear_model(https://justkode.kr/machine-learning/linear_model)에 했던, LinearRegression() 객체와 상당히 비슷한 것을 알 수 있습니다.

다중 로지스틱 회귀

물론, 다중 로지스틱 회귀 또한 가능합니다. 이에 대해 간단히 설명 하자면, 다중 로지스틱 회귀는 시그모이드 함수의 개념을 진화 시킨, 소프트맥스 함수에 더 가깝습니다. 범주가 3개인 회귀 모델이라고 가정해 보겠습니다.

\log {\frac {P(Y=1|X=\vec{x})} {P(Y=3|X=\vec{x})}} = \beta_{1}^T\vec {x}

\log {\frac {P(Y=2|X=\vec{x})} {P(Y=3|X=\vec{x})}} = \beta_{2}^T\vec {x}

이를 이항하여 정리하면, 다음과 같습니다. 이러한 연산과, 경사 하강법을 통해 답에 점점 가까워 지도록 파라미터가 학습 됩니다.

P(Y=1|X=\vec{x}) = \frac {e^{\vec{\beta_{1}}^T\vec {x}}} {1 + e^{\vec{\beta_{1}}^T\vec {x}} + e^{\vec{\beta_{2}}^T\vec {x}}}

P(Y=2|X=\vec{x}) = \frac {e^{\vec{\beta_{2}}^T\vec {x}}} {1 + e^{\vec{\beta_{1}}^T\vec {x}} + e^{\vec{\beta_{2}}^T\vec {x}}}

P(Y=3|X=\vec{x}) = \frac {1} {1 + e^{\vec{\beta_{1}}^T\vec {x}} + e^{\vec{\beta_{2}}^T\vec {x}}}

다항 로지스틱 회귀 예시 코드

위에서 한 이항 로지스틱 회귀 코드와 유사합니다. 범주가 4개로 늘어남에 따라, 코드를 수정하였고, 다항 로지스틱 회귀를 위해 coef_ 어트리뷰트의 차원 수가 증가 했음을 알 수 있습니다.

데이터 삽입

x = []
y = []

for i in range(100):
  for j in range(100):
    x.append([i, j])

x = np.array(x)
np.random.shuffle(x)

for i in range(10000):
  if x[i, 0] * 2 + x[i, 1] < 70:
    y.append(0)
  elif x[i, 0] * 2 + x[i, 1] < 140:
    y.append(1)
  elif x[i, 0] * 2 + x[i, 1] < 210:
    y.append(2)
  else:
    y.append(3)

y = np.array(y)

데이터 학습

lr = LogisticRegression().fit(x, y)
test_x = x[:30]
test_y = lr.predict(test_x[:, :])

for i in range(30):
  if test_y[i] == 0:
    plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='red')
  elif test_y[i] == 1:
    plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='blue')
  elif test_y[i] == 2:
    plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='purple')
  else:
    plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='green')

print(lr.coef_, lr.intercept_)
print(np.exp([
              np.sum(test_x[0, :] * lr.coef_[0]) + lr.intercept_[0],
              np.sum(test_x[0, :] * lr.coef_[1]) + lr.intercept_[1],
              np.sum(test_x[0, :] * lr.coef_[2]) + lr.intercept_[2],
              np.sum(test_x[0, :] * lr.coef_[3]) + lr.intercept_[3]
            ]))
print(test_y[0])
plt.show()

0번째 데이터의 확률 값을 계산 해 본 결과, 1번이 제일 높게 나옴을 확인 할 수 있습니다.

학습이 잘 된 모습

자세한 내용은 아래 링크들을 참고 해 주세요!

이론: Multinomial Logistic Regression / 위키피디아(영문)
코드: Scikit Learn Document 코드 예시
LogisticRegression 클래스: Scikit Learn API 문서

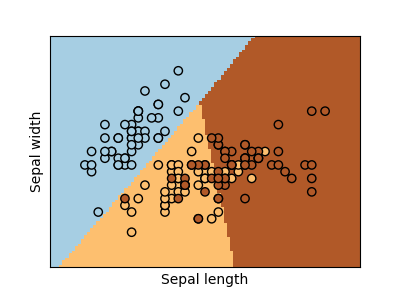
다중 로지스틱 회귀의 예시

Reference

항상 양질의 글을 제공해 주는 ratsgo님께 감사합니다.

ratsgo님의 블로그: (https://ratsgo.github.io/machine%20learning/2017/04/02/logistic/)