[찍먹 Data Science] 5. Machine Learning Basic

Maching Learning Basic.

안녕하세요? Justkode 입니다. 오늘은 머신 러닝의 기본 개념에 대해 공부 해 보는 시간을 가져 보도록 하겠습니다.

학습의 종류

머신 러닝 학습의 종류는 두 종류가 있습니다.

지도 학습 (Supervised Learning)

첫 번째는 지도 학습입니다. 지도 학습은 훈련 데이터로 **Feature(특징)**와 Target(결과) 쌍이 주어지며, 훈련 데이터로부터 하나의 함수(모델)를 유추해내기 위한 기계 학습의 하나의 방법입니다. 가장 기본적인 형태이며, Feature를 모델에 삽입하여 나오는 결과 값과 실제 결과를 비교 하는 방식으로 학습 합니다. 다시 한번 직관적으로 설명 드리자면, 주어진 데이터를 통해 결과 값을 예측하는 함수를 만든다라고 할 수 있을 것 같습니다.

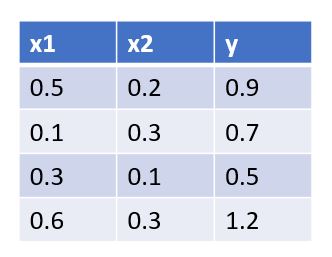
x1, x2는 Feature, y는 Target

다음은 지도 학습의 종류 대해서 알아 보겠습니다.

회귀(Regression): 회귀 문제는 한 개 이상의 독립 변수 (Feature)와 종속 변수 y (Target)와의 관계를 모델링 하여, 연속적인 결과 값을 예측하는 데에 사용 됩니다. 예시로는 부동산 가격 예측, 키를 통한 몸무게의 예측 등등이 있겠습니다.

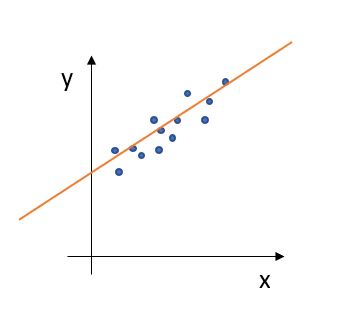
회귀의 예시

분류(Regression): 분류 문제는 한 개 이상의 독립 변수 (Feature)와 종류 y (Target)와의 관계를 모델링 하여 비연속적인 결과, 즉 분류를 목표로 합니다. 예시로는, 키와 몸무게를 통한 남/여 예측, 줄기의 길이와 너비를 통한 붓꽃 품종 예측 등이 있겠습니다.

분류의 예시

비지도 학습 (Unsupervised Learning)

두 번째는 비지도 학습입니다. 비지도 학습은 훈련 데이터로 Feature(특징) 만이 주어 집니다. "아니, 이게 무슨 의미가 있나?" 하실 수도 있지만, 비지도 학습은 데이터간 숨겨진 구조를 찾는 데 사용 됩니다.

예시를 들자면 다음과 같습니다.

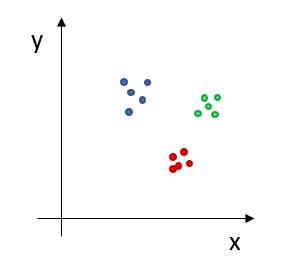
군집(Cluster): 입력된 데이터를 비슷한 것들끼지 묶는 것을 **군집화(Clustering)**이라고 하고, 이렇게 묶인 집합을 **군집(Cluster)**이라고 합니다. 이를 통해, 잡음 추출, 연관 게시글 추천등을 할 수 있습니다.

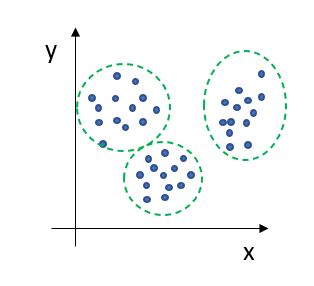
군집의 예시

차원 축소: 혹은 비지도 학습은 비슷한 Feature 관계성을 나타 내는 차원에 대해, 차원을 축소 시키는 기능을 수행 할 수 있습니다. 예로는 매니폴드 구조가 있습니다.

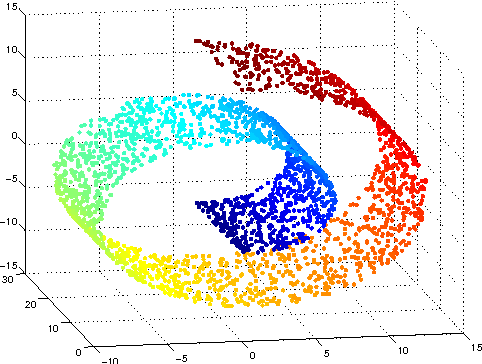
차원 촉소의 예시

Dataset의 분류

우리가 모델을 학습 시키기 위한 Dataset은 다음과 같이 분류 할 수 있습니다.

훈련 세트 (Train Set): 모델을 훈련 시키기 위해 사용 합니다.
검증 세트 (Validation Set): 모델의 일반화 성능을 검증하기 위해 사용 합니다. 여러 개의 모델을 중간 까지 학습 시킨 후, 일반화 성능이 좋은 모델을 선택하여 계속 학습 하고자 할 때 선택 합니다.
테스트 세트 (Test Set): 모델의 성능이 목표치에 달성 했을 때, 최종 평가에 사용 됩니다.

Overfitting?

Overfitting이란, 훈련 세트에 대해서는 모델이 높은 정확도를 보이나, 테스트 세트에 대해서는 낮은 정확도를 보일 때를 말합니다. 다시 말하면, 일반화 성능이 떨어짐을 의미하며, 이를 해결하기 위해선 검증 세트를 이용하여, 여러 가지 모델에 대해 일반화 성능을 평가 한 후, 일반화 성능이 더 좋은 모델을 선택하여 학습하거나, Feature의 갯수를 최소화 하거나, 더 많은 데이터 셋사용, 더 단순한 모델 사용 등이 있겠습니다.

파란색이 일반화 면에서 이상적, 빨간색처럼 Noisy한 데이터 까지 캐치 할 필요는 없다.

Cost Function (비용 함수)

우리가 학습이 잘 되었는지, 안 되었는지 어떻게 판단 할 수 있을가요? 이는 각 목적에 맞는 **비용 함수 (Cost Function)**를 사용 함으로써 알 수 있습니다. (혹은 이는 **Loss Function(손실 함수)**라고도 불립니다.)

만약 우리가 회귀에 대해서 학습이 잘 되었는지 수치적 평가를 하고자 합니다. 그럴 때는 어떻게 하면 될까요? 답은 정답과 예측 값의 제곱의 합을 더함으로써, 수치의 차가 적으면 적을 수록, 학습이 잘 되었다고 판단 할 수 있습니다.

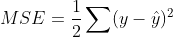
MSE (Mean Square Error)

혹은 이제 분류에 대해서 학습이 잘 되었는지 수치적 평가를 하고자 할 때는요? 그럴 때는, 해당 문제를 답으로 예측한 확률과 실제 분류의 차이 값에 로그를 씌운 값을 더함으로써 가능 합니다.

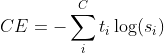
Cross-Entropy Loss, C는 클래스의 갯수, t_i는 참이면 1, 아니면 0, s_i는 예측한 확률

군집이 잘 되었는지는 어떻게 판단 할 수 있을까요? 이는 아마 군집들의 평균값과 군집 샘플과의 거리의 합이 될 수도 있겠네요.

아무튼 이런 식으로, 모델이 잘 학습 되었는지에 대한 평가를 통해, 이를 줄여 나가는 방식으로 학습하면 될 것입니다. 그런데 어떻게 학습 하냐고요..?

Gradient Descent (경사 하강법)

1강때 진행 했던 **계산 그래프(Computational Graph)**를 기억 하시나요? 계산 그래프를 이용해서, 우리는 손실 함수를 줄이는 방향으로 값을 이동하면, 이에 맞는 파라미터 또한 같이 계산 그래프에서 전달된 미분 값을 바탕으로 파라미터 값을 변경 해 주면 될 것입니다.

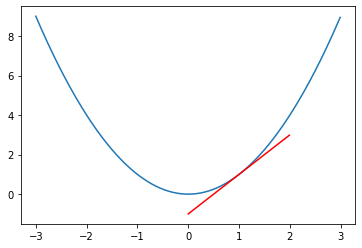
Cost Function의 미분을 구한 후, 경사를 따라 내려 감.

구한 미분 값을 바탕으로, 이를 파라미터에 전달함.

사실, 경사 하강법을 하는 방법은 매우 다양합니다. 우리가 정직하게 내려 가면, 그것은 극소에서 멈출 가능성이 높습니다.

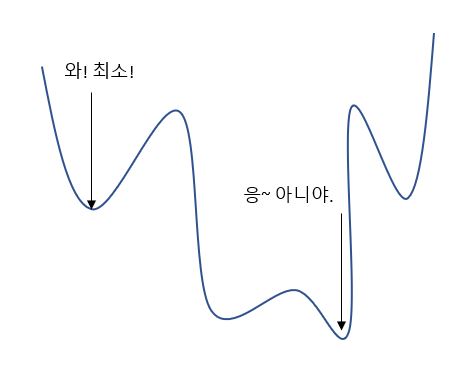
손실 함수 그래프가 이렇게 생겨 버리면..? 생각보다 킹받는 상황.

극소값에서 멈추지 않게 하기 위해, 다음과 같이 여러개의 경사 하강법을 사용 할 수 있습니다.

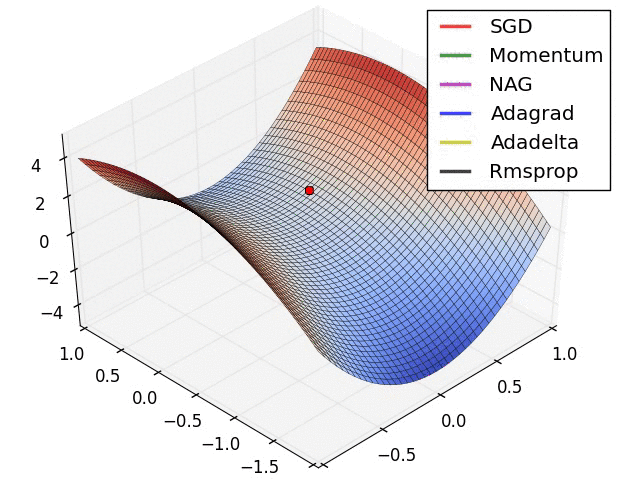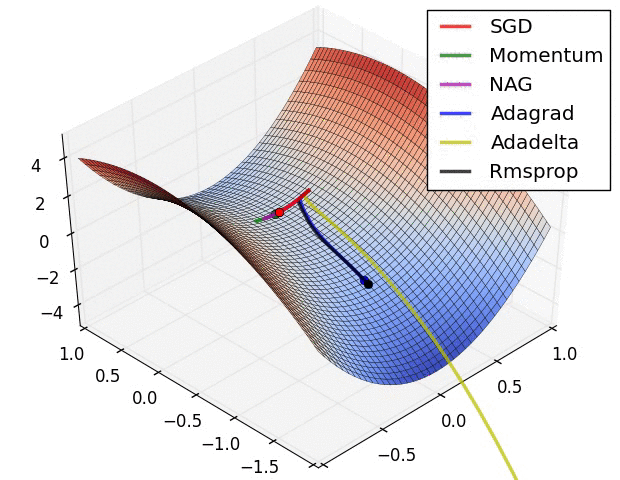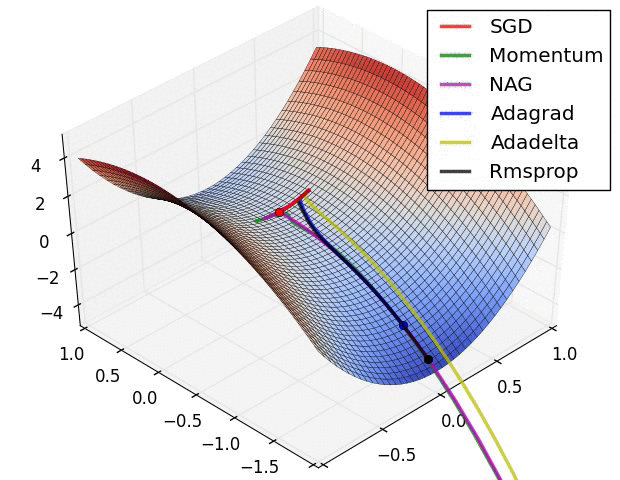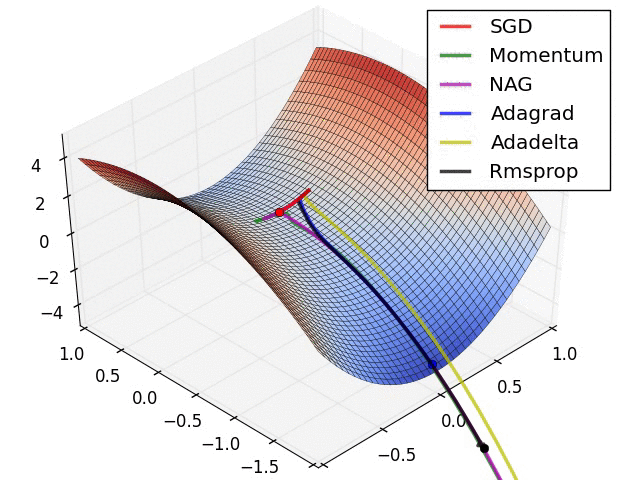
다양한 경사 하강법

배치와 미니 배치, 확률적 경사 하강법

학습을 할 때, 행렬 연산을 한꺼번에 하느냐, 나누어서 하느냐에 따라 경사 하강법의 종류가 달라집니다.

배치 경사 하강법 (Batch Gradient Descent: BGD): 배치 경사 하강법은, 전체 학습 데이터를 묶어서 학습 시키는 경사 하강법 입니다. 안정적인 수렴이 가능하지만, 속도가 느리고, 극소값에 갇힐 확률이 늘어 납니다.

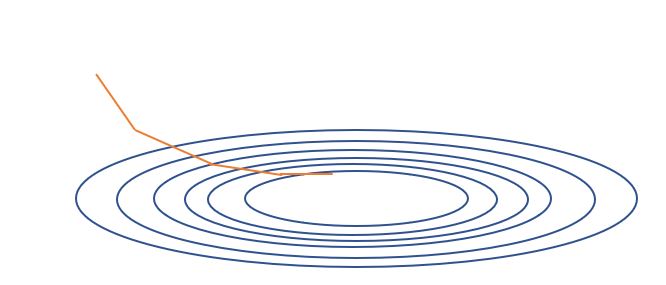
배치 경사 하강법

확률적 경사 하강법 (Stochastic Gradient Descent: SGD): 확률적 경사 하강법은 하나의 데이터 당, 한 번 학습을 진행 하는 방법으로, 극소값에 갇힐 확률이 적지만, 노이즈가 심하고, 병렬 연산에 능한 GPU를 잘 활용 할 수 없습니다.

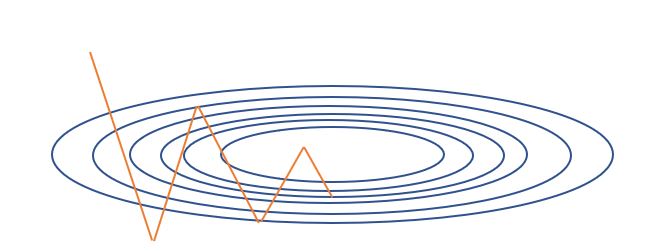
확률적 경사 하강법

미니 배치 확률적 경사 하강법 (Mini-Batch Stochastic Gradient Descent: MSGD): 미니 배치 확률적 경사 하강법은 하나의 배치를, 여러 개의 미니 배치로 쪼어 학습 하는 방식으로, 배치 경사 하강법과, 확률적 경사 하강법의 중간 경계라고 생각 할 수 있습니다.

미니 배치 확률적 경사 하강법

학습 과정

고로 기계학습의 학습 과정은 다음과 같습니다.

데이터에 맞는 적절한 모델, 손실 함수과 하이퍼 파라미터를 사용 합니다.
가지고 있는 데이터를 바탕으로 현재 모델에 대해서 손실 함수를 계산합니다.
손실 함수가 낮아지는 방향으로 경사 하강법을 진행 합니다.
2 ~ 3번의 과정을 원하는 결과 (정확도)가 나올 때 까지 반복 합니다.
(검증 데이터셋이 있고, 여러 개의 모델을 학습 중일 때) 검증 데이터 셋을 통해 일반화 성능을 비교 하고, 좋은 일반화 성능을 가진 모델을 원하는 결과가 나올 때 까지, 다시 학습 합니다.
테스트 데이터 셋으로 검증합니다.

마치며

이번 시간에는 머신 러닝의 필수 기본 개념에 대해서 배워 보았습니다. 다음 시간에는 선형 회귀와 로지스틱 회귀에 대해 이론을 알아 보고, scikit-learn으로 실습 하는 시간을 가져 보도록 하겠습니다.