[찍먹 Data Science] 7. SVM, K-NN, Random forest

SVM, K-NN, Random Forest

안녕하세요? Justkode 입니다. 저번 시간에는 선형 회귀와 분류에 대해 공부 해 보았습니다. 그런데 Logistic Regression을 학습 시키면서, 여러가지 의문이 들 수 있습니다.

"그런데 만약 학습이 그냥 경계를 만드는 데에만 멈추게 되면, 일반화 성능이 떨어 지는 거 아닐까?"
"그냥, 데이터를 분류할 때, 가장 가까운 레이블에 분류하면 빠르게 분류 할 수 있지 않을까?"
"간단하고, Overfitting이 잘 되지 않는 모델을 만들 수 없을까?"

이는 각각 SVM, K-NN, Random Forest를 통해서 해결 할 수 있습니다.

Before we start

먼저 이번 실습에는 scikit-learn 모듈이 필요합니다. 다음을 통해 설치 해 주세요. (단, numpy, pandas, matplotlib이 설치 되어 있다면 scikit-learn만 설치 하셔도 됩니다.)

pip install numpy
pip install pandas
pip install -U matplotlib
pip install -U scikit-learn

SVM (Support Vector Machine)

먼저, SVM에 대해서 알아 보는 시간을 가져 보도록 하겠습니다. SVM은 주어진 데이터가 어느 카테고리에 속하는지 판단하는 이진 선형 분류 입니다.

왜 이름이 Support Vector Machine이냐 하면, 특정 분류에 해당하는 벡터를 지나는 평행한 두 직선을 그어 경계를 결정 하기 때문입니다.

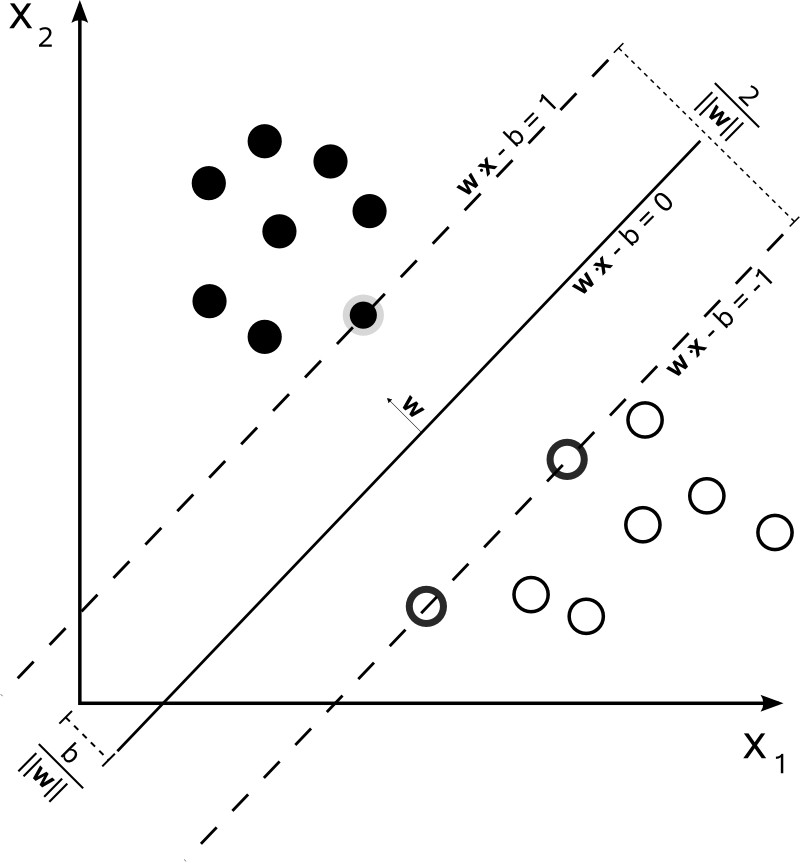
출처: 위키피디아

이것만 보면 Logistic Regression과 크게 다를 게 없어 보입니다. 하지만, 가장 큰 차이점이 있다면, Cost Function에서 Margin을 고려 한다는 것입니다. 일단, 많은 수학 식들이 있기는 하지만, 이 포스트에서는 경계를 결정하는 식과 Cost Function만 설명 하도록 하겠습니다.

y의 샘플의 범주를 1, -1 이라고 가정 하면 식을 다음과 같이 나타 낼 수 있습니다.

y_i(w^Tx_i + b) \geq 1 - \xi

일단 $w$ 는 가중치, $y_i$ 는 i번째 y의 샘플, $x_i$ 는 i번째 x의 샘플, $b$ 는 편향입니다. $y_i(w^Tx_i + b) \geq 1$ 이 성립 한다는 것은, 마진 경계 내에 샘플이 존재 한다는 것을 의미 합니다. 여기서 새로 생긴 $\xi$ 변수는 슬랙 변수이며, Soft Margin SVM에 사용 되는 변수로, 마진 경계 외에서도, 샘플을 허용하기 위해 만들어 졌습니다.

자, 이를 다시 이야기하면, $\xi$ 변수가 크면 클 수록, 마진 경계를 벗어나도 정답이라고 샘플을 허용 하는 정도가 높아 진다고 볼 수 있습니다.

Cost Function

비용 함수는 다음과 같습니다. 여기서 $C$ 계수가 등장 하는데요, 이는, 슬랙 변수가 Cost Function에 영향을 주는 정도를 조정 합니다. 즉, $C$ 계수가 높으면 높을 수록 Hard Margin에 가까워 집니다.

J(w) = \frac{1}{2\left \| w \right \|} + C\sum ^n _{i=1}\xi_{i}

Code Implementation

일단 필요한 모듈을 모두 import 해 줍니다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn

첫 번째로 Train Data, Test Data를 만들어 줍니다.

train_x_0 = np.random.randn(30, 2) + np.array([1, 1])  # 평균 1, 1
train_y_0 = np.array([0] * 30)

train_x_1 = np.random.randn(30, 2) + np.array([3, 3])  # 평균 3, 3
train_y_1 = np.array([1] * 30)

test_x = np.random.randn(30, 2) + np.array([2, 2])  # 평균 2, 2

for i in range(30):
    plt.scatter(train_x_0[i][0], train_x_0[i][1], color='red')
    plt.scatter(train_x_1[i][0], train_x_1[i][1], color='blue')

plt.xlim(0, 5)
plt.ylim(0, 5)
plt.show()

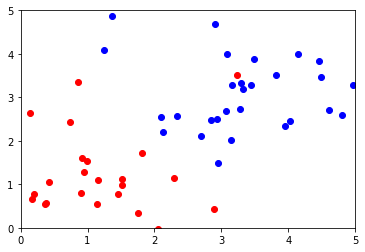
Train Data

이렇게 Data를 만들어 주었다면, 그 다음에는 데이터를 학습 시켜 줄 차례입니다. sklearn.svm 내의 SVC 모델을 이용하여, 학습을 진행 합니다. 또한, 데이터 시각화도 진행 해 봅니다.

from sklearn.svm import SVC

train_x = np.append(train_x_0, train_x_1, axis=0)  # 만들어준 train_x_0, train_x_1을 병합,
train_y = np.append(train_y_0, train_y_1)

svm = SVC(kernel='linear', C=2)
svm.fit(train_x, train_y)

plt.xlim(0, 5)
plt.ylim(0, 5)

for i in range(30):
    plt.scatter(train_x_0[i][0], train_x_0[i][1], color='red')
    plt.scatter(train_x_1[i][0], train_x_1[i][1], color='blue')
    
xx = np.linspace(0, 5, 21)  # [0, 0.25 ... , 4.75, 5]
yy = np.linspace(0, 5, 21)  # [0, 0.25 ... , 4.75, 5]
YY, XX = np.meshgrid(yy, xx)  # plt.contour 와 같이 사용, 둘이 같이 사용하여 grid 형태의 xx, yy의 쌍을 만들어 줌.
xy = np.vstack([XX.ravel(), YY.ravel()]).T  # XX.ravel == X.reshape(-1), np.vstack로 차원 변환 시켜, 스택을 만들어 줌.
Z = svm.decision_function(xy).reshape(XX.shape)  # decision_function을 이용 해서 값 추출 후 원래 모양으로 reshape.

test_y = svm.predict(test_x)  # 예측

for i in range(10):
    if test_y[i] == 0:
        plt.scatter(test_x[i][0], test_x[i][1], color='red', marker='x')
    else:
        plt.scatter(test_x[i][0], test_x[i][1], color='blue', marker='x')

plt.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])  # 경계선 그림

plt.show()

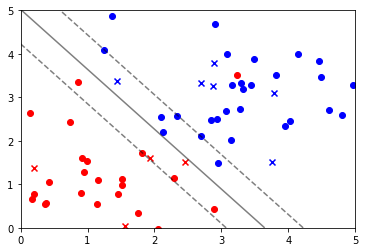
Noisy한 데이터에도 학습이 잘 된 모습

K-NN (K - Nearest Neighbor)

이 알고리즘은 매우 간단한 알고리즘 입니다. 특징 공간 내에서 그저, 가장 가까운 k개를 뽑아, k개 중 가장 많은 샘플들이 있는 레이블에 분류 됩니다. (그 이유 때문에, k의 값은 홀수가 권장 됩니다.) 이 알고리즘은 일단 학습 데이터에 타겟 값이 존재한다는 점에서 군집(Clustering)과 다릅니다. 거리를 측정 할 때에는 유클리디안 거리 ( $\sqrt{x_1^2 + x_2^2 + ... + x_n^2}$ )를 계산하여, 가장 가까운 k개를 선정 합니다.

또 다른 흥미로운 점은, 이 친구는 Cost Function이 없습니다.

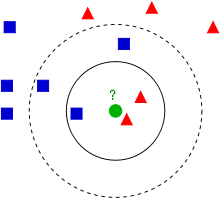
출처: 위키 피디아, k = 3일시 빨강, k = 5일시 파랑으로 분류 된다.

Code Implementation

from sklearn.neighbors import KNeighborsClassifier
from matplotlib.colors import ListedColormap

train_x_0 = np.random.randn(30, 2) + np.array([-5, -5])  # 평균 5, 5
train_y_0 = np.array([0] * 30)

train_x_1 = np.random.randn(30, 2) + np.array([5, 5])  # 평균 -5, -5
train_y_1 = np.array([1] * 30)

train_x = np.append(train_x_0, train_x_1, axis=0)
train_y = np.append(train_y_0, train_y_1)

neigh = KNeighborsClassifier(n_neighbors=3)  # k 갯수를 3으로
neigh.fit(train_x, train_y)

xx, yy = np.meshgrid(np.arange(-8, 8, .1), np.arange(-8, 8, .1))
Z = neigh.predict(np.c_[xx.ravel(), yy.ravel()])  # np.c_로 위아래로 행렬 붙임

# Put the result into a color plot
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])  # [0, 1, 2]에 대해 색상 적용
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=cmap_light)  # z에 따라 적용 함

for i in range(30):
    plt.scatter(train_x_0[i][0], train_x_0[i][1], color='red')
    plt.scatter(train_x_1[i][0], train_x_1[i][1], color='blue')

plt.xlim(-8, 8)
plt.ylim(-8, 8)
plt.show()

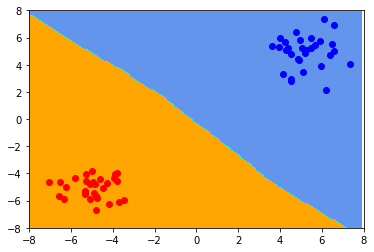
Decision Boundary가 형성 된 모습

Random Forest

Random Forest는 여러 개의 모델을 합쳐 놓은 앙상블 모델 (ensemble model) 입니다. 아, 일단 이름이 왜 Random Forest냐면, 여러 개의 Decision Tree가 모여서, Forest를 만든다고 하여 Random Forest 입니다.

학습 과정은 다음과 같습니다.

Decision Tree는 입력 Feature중, 몇 개의 Feature만 골라서 의사 결정을 실시 합니다. 이렇게 몇 개의 Feature 만을 고르는 이유는 Overfitting의 방지와 Tree의 다양성을 위해서 입니다.
여러 개의 Tree는 입력 Feature에 대해, Target 예측을 실시 합니다. 여기서, 가장 많이 Target으로 예측 된 값을 정답으로 선정합니다.
선정 된 값과 실제 값을 비교 한 후, 안 좋은 성능을 내는 Decision Tree에 대해서는 가지 치기를 하고, 새로운 Tree를 생성 합니다.
적절한 값이 나올 때 까지 반복 합니다.

이 알고리즘에 대한 장점이 있다면 Numerical 하게 데이터를 바꿀 필요가 없다는 것! 범주형 데이터, 숫자형 데이터에 대해 모두 적절 한 분류를 시행 합니다.

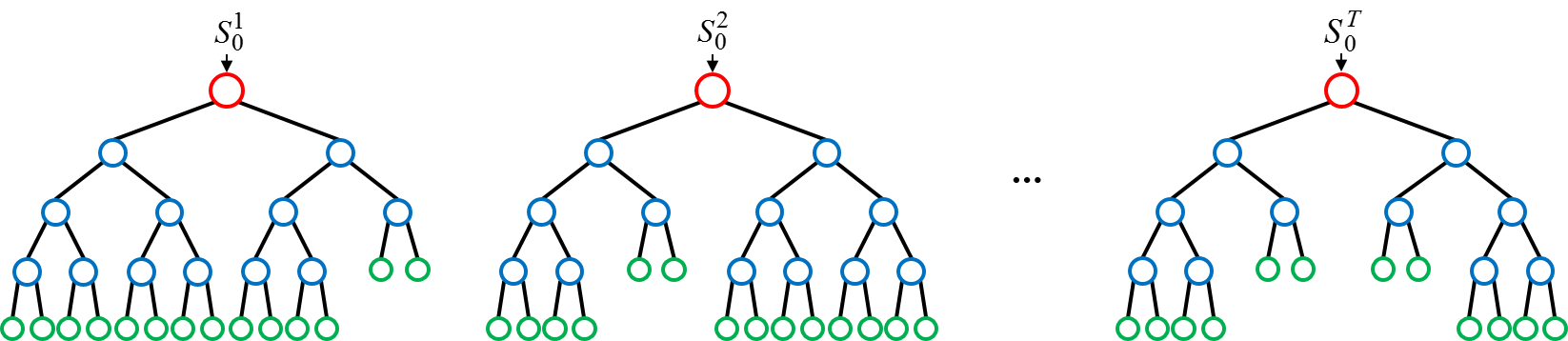
여러 Tree에 대해 "투표"를 받는 모습. 각 노드가 하나의 질문이라고 생각하면 됨. (ex: a > 5 인가?, b == "한국" 인가?)

Code Implementation

load_wine 데이터를 통해, 와인의 종류를 분류 하는 Random Forest 모델을 만들어 보겠습니다. sklearn.ensemble내의 RandomForestClassifier 모델을 사용 합니다.

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine

wine = load_wine()  # X가 13개의 feature, 시각화 어려움
X = wine.data
Y = wine.target

X_train, X_test = X[:-30], X[-30:]
Y_train, Y_test = Y[:-30], Y[-30:]

forest = RandomForestClassifier(n_estimators=100, random_state=0) # n_estimators: 사용할 tree 갯수
forest.fit(X_train, Y_train)

accuracy = (sum(forest.predict(X_test) == Y_test) / 30) * 100  # numpy의 boolean 연산을 통한 확률 계산

print(f"정확도: {accuracy}%")

1개 빼고 모든 분류를 잘 해낸 모습을 볼 수 있습니다.

정확도: 96.66666666666667%

각 요소의 중요도

각 요소의 중요도는 RandomForestClassifier 객체 내의 feature_importances_ 어트리뷰트를 이용 합니다.

forest.feature_importances_

array([0.16453422, 0.03106235, 0.01829371, 0.03240328, 0.04474084,
       0.04180306, 0.13492073, 0.01458841, 0.05394241, 0.16223051,
       0.04170749, 0.0540259 , 0.2057471 ])

마치며

이번 시간에는 SVM, K-NN, Random forest에 대해서 배워 보았습니다. 오늘 배운 모델들은 가벼우면서 실무에서 많이 쓰이는 모델들 이므로, 여기서 "찍먹" 수준에서 머물지 않고, 더 깊게 배우셨으면 하는 마음입니다. 다음 시간에는 **Normalization (정규화), PCA (차원 축소)**에 대해 이론을 알아 보고, 정규화를 이용하는 이유를 수학적인 관점에서 파악해 보고, 정규화를 실시 하여 보며, PCA를 이용하여 정보의 손실을 최소화 하며 차원을 축소 시켜보는 실습을 진행 해 보겠습니다.