[찍먹 Data Science] 8. Normalization, PCA

Normalization, PCA

안녕하세요? Justkode 입니다. 이번 시간에는 **Normalization (정규화)**와, 차원 축소를 위한 PCA에 대해 공부 해 보는 시간을 가져 보도록 하겠습니다. 정규화와 차원 축소는 기계 학습에서 중요 한 요소 입니다. 학습에서 직접적인 영향을 주기 때문이죠.

Normalization

저번에 Linear Regression의 Cost Function에 대한 미분을 하게 되면, Input Vector가 나온다는 말을 한적이 있습니다. 다음과 같이 말이죠.

\frac{\partial MSE}{\partial w} = \frac{2}{m}\sum_{i}^{C}(\hat{y} - y)X

만약 $X = \begin{bmatrix} x_0 & x_1 & ... & x_n \end{bmatrix}^T$ 라고 가정 하면, 식을 보면 알다 싶이, 특정 feature의 범위가 0~~100, 0~~1 이렇게 들쑥 날쑥하게 되면, 똑같은 학습률을 바탕으로, 다른 정도로 학습이 되기 때문에 정규화 과정이 필요 합니다.

Min - Max 정규화

일단 첫 번째로는 Min - Max 정규화가 있습니다. 데이터를 최솟값과 최고값을 이용하여 정규화 하는 방법이며, 이렇게 정규화를 진행 하면 데이터의 범위가 [0, 1] 로 변하게 됩니다.

\frac{X - X_{min}} {X_{max} - X_{min}}

이를 코드로 구현 하면 다음과 같습니다. numpy.ndarray를 정규화 한다고 가정 하겠습니다.

Module Import

import numpy as np
import pandas as pd

before_n = np.random.normal(0, 10, size=(10,))
before_n

Out: 정규화 전

array([ -7.60552157,  -7.4768014 ,   3.58856804,  -8.64994768,
        -5.43849334,  11.49147181,   0.71011417,  -1.98272815,
       -10.6252785 , -14.26019951])

after_n = (before_n - before_n.min()) / (before_n.max() - before_n.min())
after_n  # numpy의 Broadcast를 이용하여 간편하게 구현 가능.

array([0.25841732, 0.26341584, 0.69311103, 0.21785972, 0.3425683 ,
       1.        , 0.58133367, 0.47676406, 0.14115282, 0.        ])

Z-Score Normalization

두 번째는 Z-Score Normalization 입니다. 이는 입력 데이터의 표준 편차와 평균을 이용하여 구할 수 있습니다. 이를 통해 정규화를 진행 하면, 데이터를 중간으로 모으는 효과를 가질 수 있습니다.

\frac {Z - \mu} {\sigma}

이를 코드로 구현 하면 다음과 같습니다. numpy.ndarray를 정규화 한다고 가정 하겠습니다.

before_n = np.random.normal(5, 10, size=(10,))
before_n

Out: 정규화 전

array([  3.88259694, -12.78964916,  11.31123123,  -1.39481419,
        12.67724562,  12.82906507,   6.78477706,  -3.9266831 ,
        26.89122036,  13.87650172])

after_n = (before_n - before_n.mean()) / before_n.std()  # mean(): 평균, std(): 표준편차
after_n

array([-0.29603595, -1.87211833,  0.40621733, -0.79492702,  0.53535118,
        0.54970317, -0.0216833 , -1.03427294,  1.87904506,  0.64872081])

PCA (Principal Component Analysis)

PCA를 한국 말로 나타내면 주성분 분석 입니다. 이는 분포된 데이터들을 통해, 분포의 주성분을 찾아 줌으로써, 가장 큰 분산을 가진 주성분 (분산이 클 수록, 차원을 이동하더라도 정보의 손실이 적음)에 대해 사영 함으로써, 데이터의 차원을 줄이는 방법 중 하나 입니다.

numpy 만으로 구현하기

일단 코드를 먼저 보여 드리겠습니다. np.random.multivariate_normal 를 이용하여, [5, 5]를 평균으로 하고 [[1, 2], [2, 1]] 의 Covariance Matrix를 가지는 50개의 샘플을 만들어 보겠습니다.

import matplotlib.pyplot as plt

array = np.random.multivariate_normal([5, 5], [[1, 2], [2, 1]], 50)
plt.xlim(-5, 10)
plt.ylim(-5, 10)
plt.scatter(array.T[0], array.T[1])
plt.show()

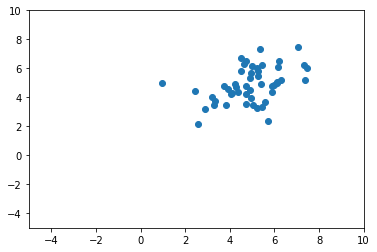
초기 데이터

그 다음, 샘플들을 Broadcasting 을 이용하여, 데이터를 원점으로 모아 줍니다.

array -= np.array([array.T[0].mean(), array.T[1].mean()])

plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.scatter(array.T[0], array.T[1])
plt.show()

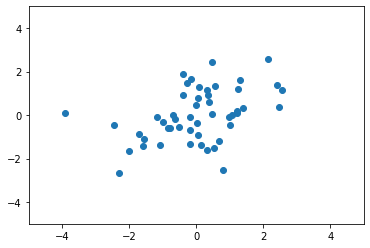
중앙으로 모아줌

그 다음, 생성된 데이터에 대한 Covariance Matrix를 구하고, 이에 대한 고유 벡터와 고유값을 구해 줍니다. 여기서 고유값이 높다는 것은, 이에 대응하는 **고유 벡터 (혹은 주성분)**에 각 Input Vector를 사영 할때, 얼마나 분산이 높은지? 그리하여, 어떻게 정보의 손실없이 사영할 수 있는 지를 나타냅니다. 다시 한번 정리 하자면, 고윳값이 높을 수록, 이에 대응하는 고유벡터를 주성분으로 삼았을 때, 정보의 손실이 작다는 것을 의미 합니다.

cov = np.cov(array.T)
eigen_val, eigen_vec = np.linalg.eig(cov)

plt.scatter(array.T[0], array.T[1])
plt.quiver([0, 0], [0, 0], eigen_vec[:, 0], eigen_vec[:, 1], color=['r', 'b'], scale=3)

print("eigenvalue: ", eigen_val)
print("eigenvector: ", eigen_vec)

eigenvalue:  [2.24427897 0.89684849]
eigenvector:  [[ 0.76269005 -0.64676417]
 [ 0.64676417  0.76269005]]

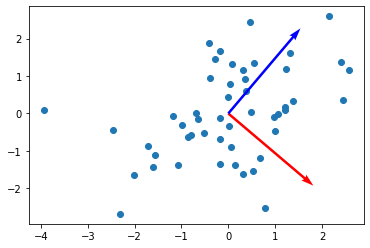
Eigenvector == 주성분

마지막으로, 해당 주성분에 벡터들을 사영을 해주면 완성이 됩니다. argmax() 메서드를 이용하여, 주 성분으로 뽑을 고유 벡터를 선택합니다.

index = eigen_val.argmax()
v = eigen_vec[index, :]  # norm: 1

result = array.dot(v) * v.reshape(-1, 1)
plt.scatter(result[0], result[1], color='green')
plt.scatter(array.T[0], array.T[1])
plt.quiver(0, 0, v[0], v[1], color='black', scale=4)
plt.xlim(-4, 4)
plt.ylim(-4, 4)
plt.show()

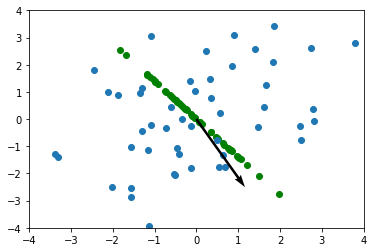
사영 한 모습

sklearn으로 더 쉽게 구현하기

이는 Scikit-Learn으로 더 쉽게 구현 할 수 있습니다. sklearn.decomposition 내의 PCA를 이용합니다. n_components를 이용 하여, 몇 차원으로 줄이고 싶은지 입력 할 수 있습니다.

from sklearn.decomposition import PCA

pca = PCA(n_components=1)  # 차원 수 1개
pca.fit(array)

print('고유 값 :', pca.explained_variance_)  # 고윳값
print('고유 벡터 :', pca.components_.T)  # 고유 벡터
print('사영 후:', pca.transform(array))

고유 값 : [2.6328486]
고유 벡터 : [[0.81183442]
 [0.58388772]]
사영 후: [[ 1.1017955 ]
 [ 1.90965349]
 [-1.26196986]
 [ 0.47308556]
 ...
 [ 0.83702101]
 [-1.95731602]]

마치며

이번 시간에는 Normalization, PCA에 다뤄 보았습니다. 다음 시간에는 딥러닝의 제일 기본이 되는, DNN에 대해 공부해 보는 시간을 가져 보도록 하겠습니다.